Get evaluation access

Table of Contents

1.1 Introduction to algorithm analysis
1.2 Analyzing algorithms
1.3 A quick mathematical review
1.4 A case study in algorithm analysis
1.5 Amortization
1.6 Exercises
1.7 Chapter notes

2.1 Introduction to basic data structures
2.2 Stacks and queues
2.3 Lists
2.4 Trees
2.5 Exercises
2.6 Chapter notes

3.1 Introduction to binary search trees
3.2 Searches and updates
3.3 Range queries
3.4 Index-based searching
3.5 Randomly constructed search trees
3.6 Exercises
3.7 Chapter notes

4.1 Introduction to balanced binary search trees
4.2 Ranks and rotations
4.3 AVL trees
4.4 Red-black trees
4.5 Weak AVL trees
4.6 Splay trees
4.7 Exercises
4.8 Chapter notes

5.1 Introduction to priority queue and heaps
5.2 Priority queues
5.3 PQ-sort, selection-sort, and insertion-sort
5.4 Heaps
5.5 Heap-sort
5.6 Extending priority queues
5.7 Exercises
5.8 Chapter notes

6.1 Introduction to hash tables
6.2 Maps
6.3 Hash functions
6.4 Handling collisions and rehashing
6.5 Cuckoo hashing
6.6 Universal hashing
6.7 Exercises
6.8 Chapter notes

7.1 Introduction to union-find structures
7.2 Union-find and its applications
7.3 A list-based implementation
7.4 A tree-based implementation
7.5 Exercises
7.6 Chapter notes

8.1 Introduction to merge-sort and quick sort
8.2 Merge-sort
8.3 Quick-sort
8.4 A lower bound on comparison-based sorting
8.5 Exercises
8.6 Chapter notes

9.1 Introduction to fast sorting and selection
9.2 Bucket-sort and radix-sort
9.3 Selection
9.4 Weighted medians
9.5 Exercises
9.6 Chapter notes

10.1 Introduction to the greedy method
10.2 The fractional knapsack problem
10.3 Task scheduling
10.4 Text compression and Huffman coding
10.5 Exercises
10.6 Chapter notes

11.1 Introduction to divide-and-conquer
11.2 Recurrences and the master theorem
11.3 Integer multiplication
11.4 Matrix multiplication
11.5 The maxima-set problem
11.6 Exercises
11.7 Chapter notes

12.1 Introduction to dynamic programming
12.2 Manufacturing costs
12.3 The longest common subsequence problem
12.4 The general technique
12.5 Telescope scheduling
12.6 Matrix chain-products
12.7 Game strategies
12.8 The 0-1 knapsack problem
12.9 Exercises
12.10 Chapter notes

13.1 Introduction to graphs and traversals
13.2 Graph terminology and representations
13.3 Depth-first search
13.4 Breadth-first search
13.5 Transitive closure
13.6 Directed acyclic graphs
13.7 Biconnected components
13.8 Exercises
13.9 Chapter notes

14.1 Introduction to shortest paths
14.2 Single-source shortest paths
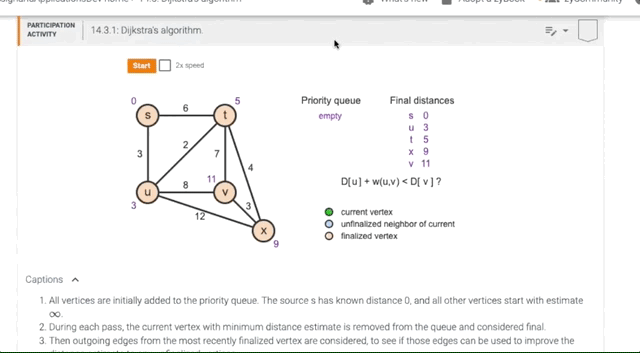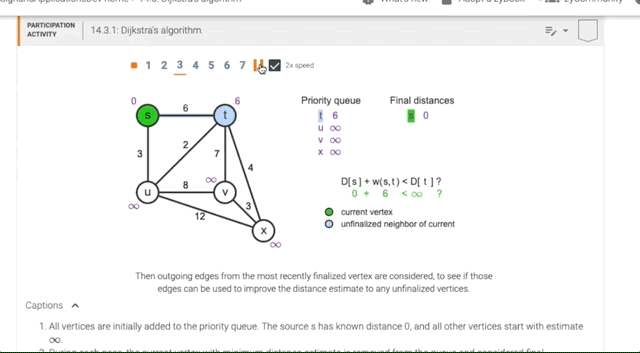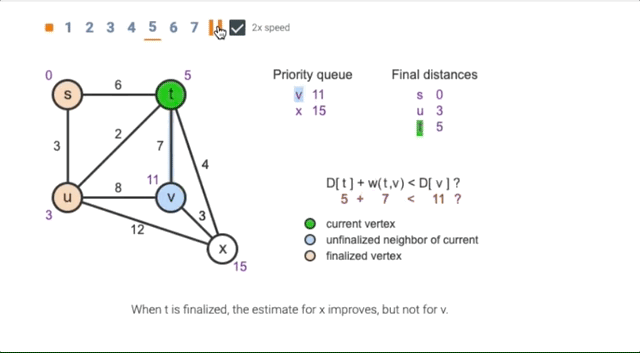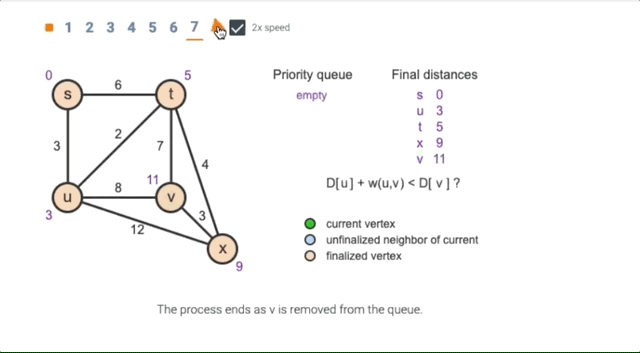
14.3 Dijkstra’s algorithm
14.4 The Bellman-Ford algorithm
14.5 Shortest paths in directed acyclic graphs
14.6 All-pairs shortest paths
14.7 Exercises
14.8 Chapter notes

15.1 Introduction to minimum spanning trees
15.2 Properties of minimum spanning trees
15.3 Kruskal’s algorithm
15.4 The Prim-Jarník algorithm
15.5 Barůvka’s algorithm
15.6 Exercises
15.7 Chapter notes

16.1 Introduction to network flow and matching
16.2 Flows and cuts
16.3 Maximum flow algorithms
16.4 Maximum bipartite matching
16.5 Baseball elimination
16.6 Minimum-cost flow
16.7 Exercises
16.8 Chapter notes

17.1 Introduction to NP-completeness
17.2 P and NP
17.3 NP-completeness
17.4 CNF-SAT and 3SAT
17.5 Vertex-cover, clique, and set-cover
17.6 Subset-sum and knapsack
17.7 Hamiltonian-cycle and TSP
17.8 Exercises
17.9 Chapter notes

18.1 Introduction to approximation algorithms
18.2 The metric traveling salesperson problem
18.3 Approximations for covering problems
18.4 Polynomial-time approximation schemes
18.5 Backtracking and branch-and-bound
18.6 Exercises
18.7 Chapter notes

19.1 Introduction to randomized algorithms
19.2 Generating random permutations
19.3 Stable matching and coupon collecting
19.4 Minimum cuts
19.5 Finding prime numbers
19.6 Chernoff bounds
19.7 Skip lists
19.8 Exercises
19.9 Chapter notes

20.1 Introduction to B-trees and external memory
20.2 External memory
20.3 (2,4) trees and B-trees
20.4 External-memory sorting
20.5 Online caching algorithms
20.6 Exercises
20.7 Chapter notes

21.1 Introduction to multidimensional searching
21.2 Range trees
21.3 Priority search trees
21.4 Quadtrees and k-d trees
21.5 Exercises
21.6 Chapter notes

22.1 Introduction to computational geometry
22.2 Operations on geometric objects
22.3 Convex hulls
22.4 Segment intersection
22.5 Finding a closest pair of points
22.6 Exercises
22.7 Chapter notes

23.1 Introduction to string algorithms
23.2 String operations
23.3 The Boyer-Moore algorithm
23.4 The Knuth-Morris-Pratt algorithm
23.5 Hash-based lexicon matching
23.6 Tries
23.7 Exercises
23.8 Chapter notes

24.1 Introduction to cryptography
24.2 Greatest common divisors (GCD)
24.3 Modular arithmetic
24.4 Cryptographic operations
24.5 The RSA cryptosystem
24.6 The El Gamal cryptosystem
24.7 Exercises
24.8 Chapter notes

25.1 Introduction to the fast Fourier transform
25.2 Convolution
25.3 Primitive roots of unity
25.4 The discrete Fourier transform
25.5 The fast Fourier transform algorithm
25.6 Exercises
25.7 Chapter notes

26.1 Introduction to linear programming
26.2 Formulating the problem
26.3 The simplex method
26.4 Duality
26.5 Applications of linear programming
26.6 Exercises
26.7 Chapter notes

27.1 Introduction
27.2 Logarithms and exponents
27.3 Integer functions and relations
27.4 Summations
27.5 Useful mathematical techniques

28.1 Bibliography

The zyBooks version of Algorithm Design and Applications provides a powerful interactive learning experience

Algorithm Design and Applications zyVersion contains the complete content of the original plus new interactive animations and learning questions to engage students.

  • Over 70 animations to illustrate examples
  • Emphasizes both mathematical analysis and practical applications
  • Hundreds of interactive learning questions 

Animation of Dijkstra’s Algorithm

What is a zyVersion?

zyVersions are leading print titles converted and adapted to zyBooks’ interactive learning platform, allowing for a quick and easy transition to an engaging digital experience for instructors and students.

zyBooks’ web-native content helps students visualize concepts to learn faster and more effectively than with a traditional textbook. (Check out our research.)

This zyVersion of Algorithm Design and Applications benefits both students and instructors:

  • Instructor benefits
  • Customize your course by reorganizing existing content or adding your own
  • Continuous publication model updates your course with the latest content and technologies
  • Robust reporting gives you insight into students’ progress, reading and participation
  • Animations and other interactive content can be shown in presentation mode and used during a lecture
  • Student benefits
  • Learning questions and other content serve as an interactive form of reading
  • Instant feedback on labs and homework
  • Concepts come to life through extensive animations embedded into the interactive content
  • Save chapters as PDFs to reference the material at any time

Authors

Michael Goodrich, PhD 

Distinguished Professor of Computer Science / University of California, Irvine 

Roberto Tamassia, PhD 

Professor of Computer Science / Brown University

Michael Goldwasser, PhD  

Professor of Computer Science / Saint Louis University

Senior Contributor

Evan Olds
Senior Content Developer, zyBooks

Instructors: Interested in evaluating this zyVersion for your class?

Get evaluation access